[Ir a Métodos de integración] [Ir a Teorema Fundamental del Cálculo] [Ir a Cálculo de áreas] [Ir a Inicio]
| EJERCICIOS |
CÁLCULO DE INTEGRALES DEFINIDAS
Se incluyen aquí los ejercicios para calcular integrales definidas y sus respuestas
Ejercicio 1
Calcule las siguientes integrales definidas:
| a) |
b) |
c) |
| d) |
e) |
f) |
| g) |
h) |
i) |
| j) |
k) |
l) |
| m) |
| Respuestas: | a)-2 | b) |
c)
|
d) |
e)
|
f)
|
g) 24,2 | h) |
i) 1 | j)
|
k)
|
l) |
m) 0 |
Ejercicio 2
Sabiendo que:
![]() halle:
halle:
| a) |
b) |
c) |
| d) |
e) |
f) |
| Respuestas: | a) 4,6 | b) 10,8 | c) 21,9 | d) 11,95 | e) 3,45 | f) 7 |
Ejercicio 3
a) Calcule
![]() siendo
siendo .
.
b) Encuentre el valor de b
tal que ![]() .
.
c) Calcule
| Respuestas: | a)
|
b) b = - 1, b = 2 | c) |
Ejercicio 4
En la función definida gráficamente por:

se sabe que
![]() =
8 y
=
8 y ![]() = 6.
Halle:
= 6.
Halle:
a) ![]()
b) ![]() e indique qué representa.
e indique qué representa.
| Respuestas: a) - 6 b) 2, representa el área de la región entre la gráfica de f, el eje x, las rectas x= a, x= c. |
Ejercicio 5
En la función definida gráficamente por:

se sabe
que ![]() .
Halle:
.
Halle:
a) ![]() e indique qué representa
e indique qué representa
b)![]()
| Respuestas: | a)
b) |
CÁLCULO DE ÁREAS
Se incluyen aquí los ejercicios para calcular áreas y sus respuestas
Ejercicio 6
Escriba, sin calcular, una integral definida que indique el área de la región sombreada.
a) |
b) |
c)  |
d) 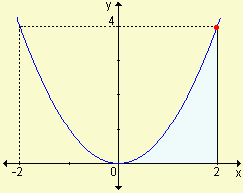 |
| Respuestas: | a)
|
b) |
| c) |
d) |
|
Ejercicio 7
En los siguientes gráficos determine el valor del área sombreada:
a) |
b) |
c) |
| Respuestas: | a)
|
b) |
c)
|
Ejercicio 8
Dada la siguiente gráfica

halle:
a) las ecuaciones de las curvas,
b) el área de la zona sombreada.
| Respuestas: | a) y = x2 , y = (x - 2)2 | b) 10 |
Ejercicio 9
Grafique la región limitada por las curvas y calcule el área determinada por ambas.
a) y = x2 con la recta y = 2x + 3
b) el eje de abscisas, la recta y = x + 1 y la recta x = 4
c) el eje de abscisas, la curva y = x2 - 1 y la recta x = 2
d) y = x2 + 2x - 1 con la recta y = - x - 1
e) y2 = 4x con la recta y = 2x - 4
f) y = lnx, el eje de abscisas y las rectas x = 2, x = 10
g) y = x2 con la recta y = 3 - 2x
h) ![]() con y =
x2
con y =
x2
i) y = 4 - x2 con la recta y = x + 2
| Respuestas: | a)
|
b) |
c)
|
d)
|
e) 9 | f) 13,64 | g)
|
h) |
i) |
Ejercicio 10
Halle el área limitada por la parábola y = 6 + 4x - x2 y el segmento determinado por los puntos A(- 2, - 6) y B(4, 6).
| Respuesta: 36 |
Ejercicio 11
Determine el área sombreada en las siguientes gráficas:
a)  |
b) |
| Respuestas: | a)
|
Ejercicio 12
Halle el área encerrada por las curvas y = x2 - 4x e y = 6x - x2 . Grafique.
| Respuesta: | el área
vale  |
Ejercicio 13
Dada la siguiente gráfica
 halle:
halle:
a) las ecuaciones de las rectas
b) el área de las zonas I y II indicadas en el gráfico.
| Respuesta: | a) |
b)
AI= 6
AII = |
Ejercicio 14
a) Calcule

b)
Determine el área de la región comprendida entre la curva y
= sen x,
el eje x y las rectas x =
-![]() y x =
y x =
![]() .
Grafique.
.
Grafique.
c) Analice por qué no se obtiene el mismo resultado en a) y b).
| Respuesta: | a) 0 b)
el área vale 2  |
c) No se puede calcular el área como la integral planteada en (a) ya que da 0 pues las dos tienen el mismo valor absoluto pero distinto signo,geométricamente la región consta de dos partes simétricas respecto del eje x. |
Ejercicio 15
Calcule el área
bajo la curva f(x)=![]() desde
0 hasta 3. Interprete gráficamente.
desde
0 hasta 3. Interprete gráficamente.
| Respuesta: | el área
vale  |
Ejercicio 16
Escriba la integral definida que proporciona el área de la región (no calcule el valor del área)

| Respuesta: | A =
|
Ejercicio 17
Halle el área limitada por la parábola y = x2 - x y la recta que une los puntos P(1, 2) y Q(- 3, - 6). Grafique.
| Respuesta: |  |
Ejercicio 18
Halle, utilizando integrales, el área del triángulo limitado por las rectas de ecuación y - 3x = 0; x - 3y = 0 y x + y = 4.
| Respuesta: | el área vale 4 |
Ejercicio 19
Calcule el área de la zona limitada por la curva y = x3 - 3x2 - x + 3 y el eje de abscisas.
| Respuesta: | el área vale 8 |
Ejercicio 20
 |
 |
 |
Halle el valor de las áreas sombreadas.
Obtenga conclusiones teniendo en cuenta que la suma de las áreas de las dos regiones coincide con el área del cuadrado de medida de lado una unidad.
Consulte la bibliografía a fin de ampliar sus conocimientos mediante la resolución de nuevos ejercicios. |
[Ir a Métodos de integración] [Ir a Teorema Fundamental del Cálculo] [Ir a Cálculo de áreas] [Ir a Inicio]